
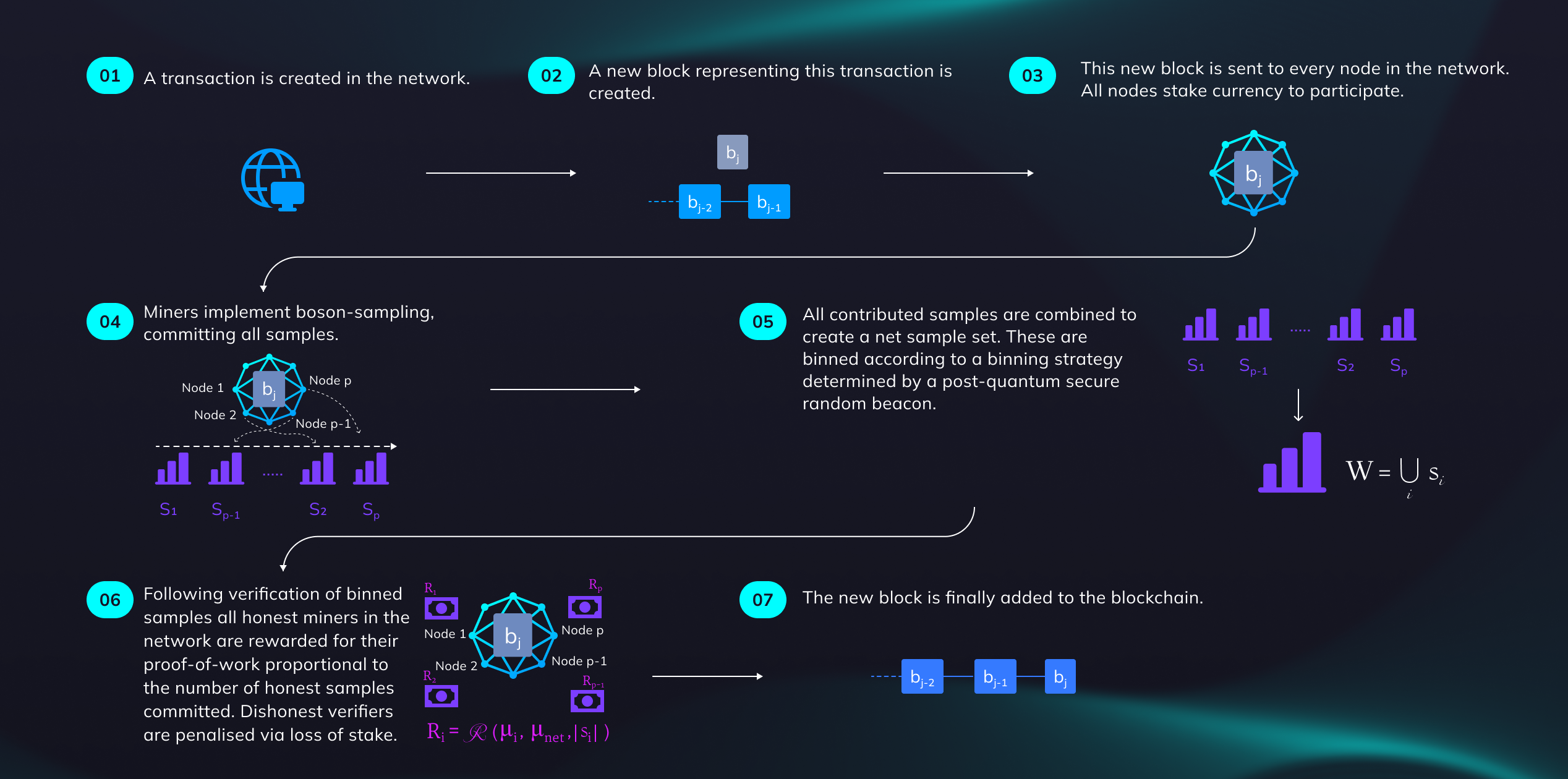
Quantum Sampling Proof-of-Work (QS-PoW), the quantum analogue to conventional proof-of-work (PoW) consensus methods, employs nodes with Noisy Intermediate Scale Quantum (NISQ) hardware to form consensus on blockchain transactions. While classical PoW (like Bitcoin) requires nodes to compete and find inputs to one-way hash functions satisfying an output constraint, QS-PoW is based on Boson Sampling. This is a relatively simple photonic quantum algorithm, readily realizable using present-day technology, where the goal is to repeatedly interfere a number of single photons in a linear optics interferometer and measure their output configuration. We use Coarse-Grained Boson Sampling (CGBS) statistics to partition the exponentially large output configurations into a polynomial number of bins.
To find a convergence in the binning statistics, a large number of samples are taken from each Boson Sampler and the output configuration is processed. Unlike raw boson sampling statistics, the binning statistics for CGBS converge under only a polynomial number of samples. Crucially, binned statistics depend on the employed binning strategy, ensuring that if samples are committed in advance of the binning strategy being decided, nodes are unable to spoof samples to reproduce a particular CGBS distribution. This is the network’s mechanism for identifying honest participants and discarding the dishonest ones.
Unlike classical PoW blockchains which expend massive amounts of energy (gas fees) in solving inverse hashing problems, BTQ’s QS-PoW scheme is energy-efficient and post-quantum secure (Figure 2) . The QS-PoW protocol’s energy consumption is determined by the number of samples each boson sampler in the network must produce. In this article, we provide network energy consumption estimates in comparison to Bitcoin’s current energy-intensive PoW protocol.
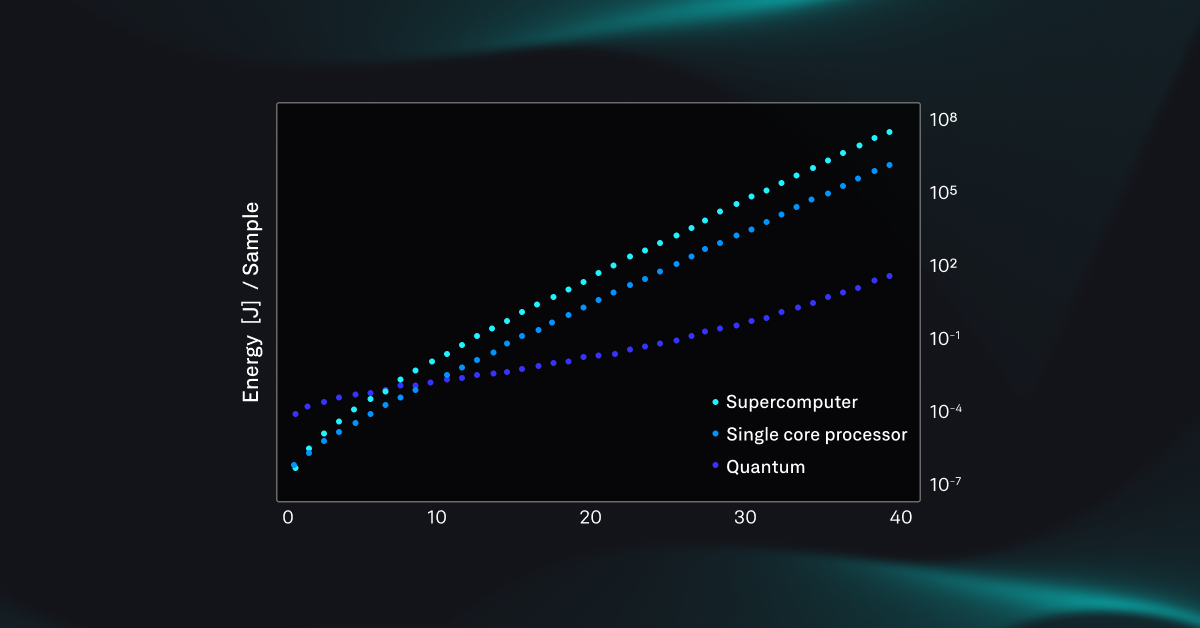
How would the energy cost of proof of work by quantum sampling (QS-PoW) compare to Nakamoto consensus in Bitcoin?
The two protocols solve different computational problems using very different kinds of processors, and of course different capital costs. But to keep things fair, let’s assume that we want the difficulty of the quantum protocol, determined by the photon number, to be set so that the time to add a new block is close to the Bitcoin network average of 10 minutes. Using the specifications for a boson sampler described here, approximately 10 million samples from the distribution on 25 photons could be collected in 10 minutes. It turns out that if every miner produces this number, it is enough to validate and reward honest miners. The total energy cost for a single quantum sampler over the block time is roughly 0.25kWh, since the main energy cost to run the device is set by the cryostat refrigerator running at ~1.5kW power. The total energy consumption of the network will therefore, depend on the number of miners participating.
To make a comparison to classical, i.e. non-quantum PoW, let’s consider that all the energy currently used in the Bitcoin network were instead devoted to QS-PoW. It turns out that the ASICs used for ultrafast hashing are totally useless for solving matrix permanents that are needed for QS-PoW, and by known computational complexity results, it is very unlikely that any ASIC could be devised to significantly speed things up. Instead the classical miners would need to use more general purpose processors. To collect 10 million samples for the 25 photon problem in 10 minutes, it would require roughly 23457 classical processors (based on each running at 3.5 GHz with 128GB RAM consuming 100W power), for a total energy cost per block per miner of 390kWh. As of Oct. 25, 2023 the Bitcoin network consumed about 1257kWh/transaction x 2000 transactions/block. If all of the Bitcoin’s network’s electricity consumption were used to perform QS-PoW using classical computers, it could support about 6450 miners. If instead all these miners were running quantum samplers, the energy savings would be a factor of about 1560 as calculated here. The simple reason is that quantum samplers are so much faster than classical computers and for time-sensitive problems like blockchains, you will need many more classical processors. Fortunately, due to nature of the quantum samplers, one can adjust the difficulty by adding a few photons without needing to upgrade the device or increase the power consumption.